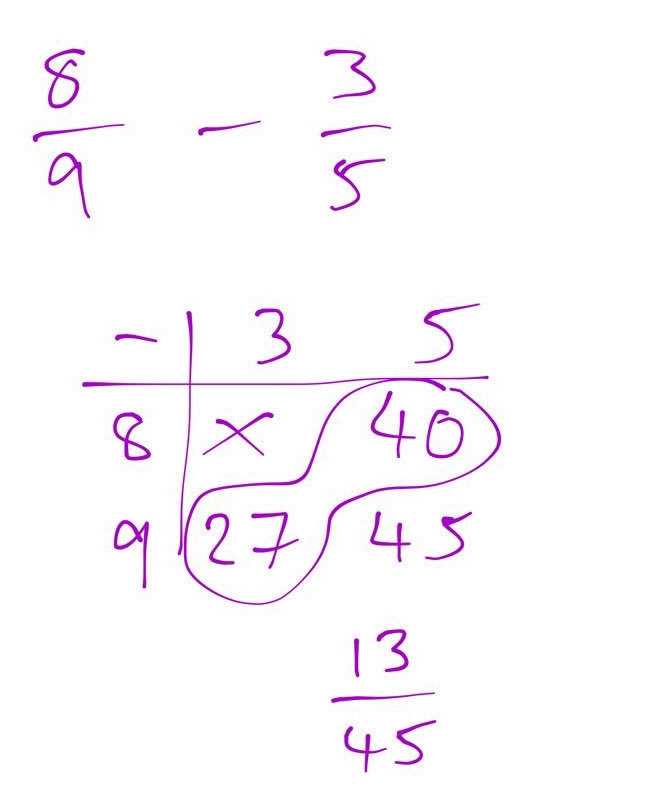
Over on Twitter, @missradders has sparked a really interesting discussion on subtracting fractions by offering the above method to subtract two fractions. (see the Twitter thread here)
I must admit, it is a method new to me and, from reading the replies to her tweet, it was unfamiliar to many other teachers, to.
But is it a valid method?
Again, reading through the comments on the thread, its taking a bit of a kicking. Before we come to a conclusion, perhaps its worth asking why, in the age of the scientific calculator, do we even bother to add or subtract fractions?
Beside me on my desk, I have the new(ish) Casio Classwiz fx-991 EX calculator, that will integrate, solve cubic inequalities, handle matrices – adding and subtracting fractions are well within its capability: what is the point of asking recalcitrant pupils to manually perform an algorithmic task that can be done electronically in moments?
The answer is algebra.
Being able to add or subtract – mentally, or on paper – straightforward fractions such as, say 3/4 – 1/2 has it’s merits, but I would be reaching for my aforementioned fancy calculator to do the subtraction at the top of the page: 8/9 – 3/5 but I need to know how to do it with numbers as it is the stepping stone to being able to work algebraically.
High end GCSE – and all A level – mathematicians need to be able to work with algebraic fractions and being secure with a method of adding and subtracting numeric fractions is crucial for this skill.
So the test of @missredders method is to see how well it works with algebraic fractions. So I tried it to subtract the fractions: a/x – b/y , my working is below.
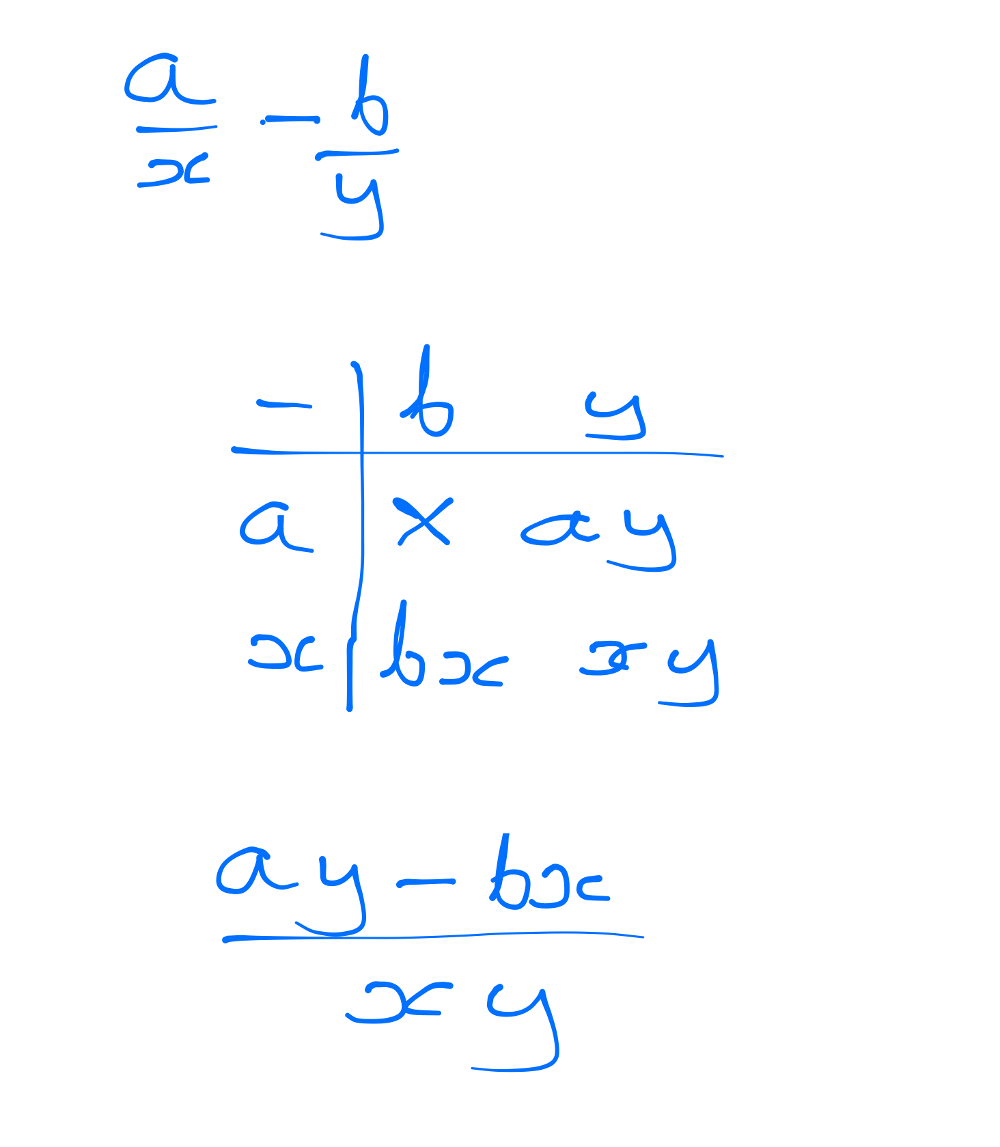
It works. In fact, I think it helps to see the method in algebraic form as it explains why it works.
I don’t think that it is a method that I will be teaching (but happy to keep it in my armoury, just in case) but I don’t think that it is the dog’s dinner that some are claiming on Twitter.
As a method it works, and there is a clear route from using the method numerically to using the method algebraically, and that is important. I suspect that if a student is taught the “grid method” shown at the top of the page, masters it and goes on to use it algebraically for higher level maths, they will probably develop their own shortcuts for using the method (i.e. going straight to writing down the common denominator) and that – find short cuts – is what maths, and being mathematical, is all about.