Numbers!

Visualising Numbers

We all see numbers differently, but I recently stumbled upon a great website for visualising numbers:

All non-prime numbers are made up of prime numbers – this is often called prime factorisation, in maths lessons we ask pupils to …

“… write [some number] as the product of its prime numbers in index form”

This great website starts at the number 1, and works its way up through the integers, in an animated dance.

The number five is shown above, this is how it shows the number 18:

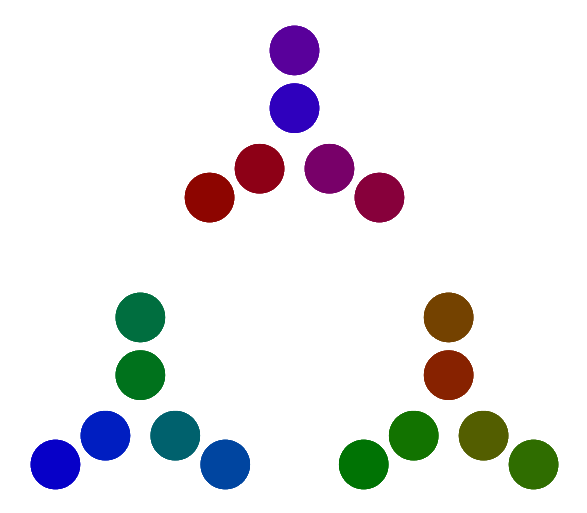can you see how its displayed?

Its shows 3 lots of 2, 3 times. Or 2 x 3 x 3 (which just happens to equal 18)

And the dance goes on and on and on …

Here’s a pic of the number 1,395 or 31 x 5 x 3 x 3:

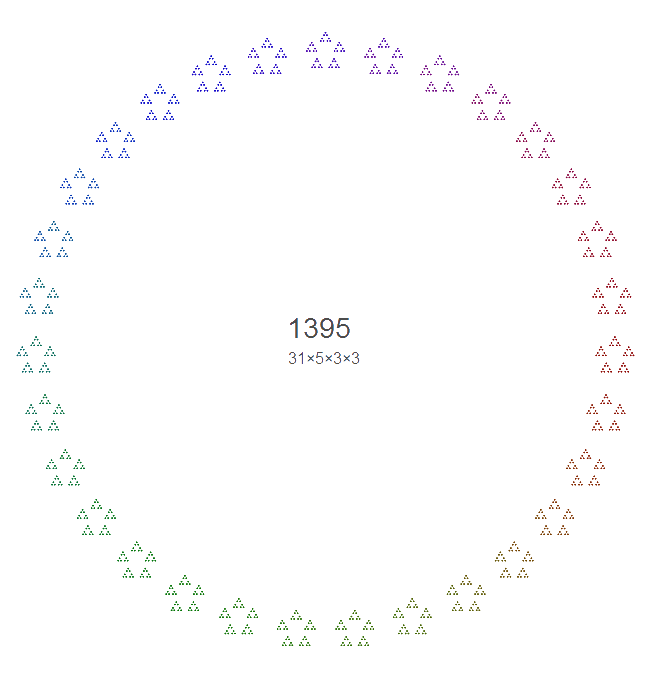It’s really quite beautiful to watch and very, very clever in the way that it breaks each number down into its prime factors.

Don’t take my word for it, visit Dance, Factors, Dance now.

Cool.