 Boxing Day. Possibly the only day I don’t envy the lifestyle of a Premier League footballer. Yes, they may earn millions, yes, they only “work” a few hours a day, but Boxing Day is a day for rest and recovery, not for running around after a ball for ninety minutes.
Boxing Day. Possibly the only day I don’t envy the lifestyle of a Premier League footballer. Yes, they may earn millions, yes, they only “work” a few hours a day, but Boxing Day is a day for rest and recovery, not for running around after a ball for ninety minutes.
So I settled down on the sofa, sports pages in hand and perused the day’s fixtures from the comfort of my own home, sporting my new fluffy slippers and wearing my Christmas jumper. Looking at the list of games I noted that the planners had done a good job of minimising the distances fans had to travel – no schleps from Sunderland to Southampton on this Boxing Day.
They had done a good job, but could they have done a better job?
Those of you who teach, or have studied, Decision Maths will be aware of the Chinese Postman algorithm for minimising the route a postmen has to take to go down every road on his beat, or the Traveling Salesman problem – finding the quickest/shortest/cheapest way of visiting every town on a route – but I’m not aware of an algorithm to minimise the collective traveling distance for fans (or teams) playing a round of fixtures.
So I made my own. Here’s what I did. First i got a mileage chart for the distance between cities in the UK, then I did the following steps:
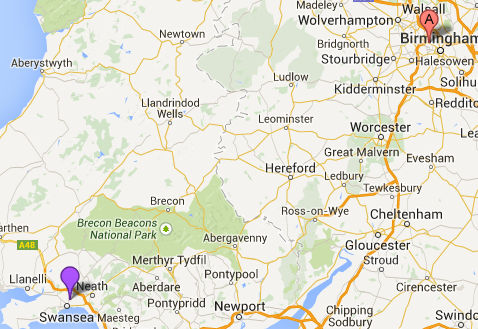
- For each team, find the nearest team to it (for example, WBA is the closest club to Swansea. But Aston Villa is the closest club to WBA etc.)
- Find the the furthest “shortest” distance (it was Swansea to WBA, circa 120 miles). Write this down as a fixture and then cross out both teams.
- Repeat steps 1 and 2 until all teams are in a fixture.
Using this method I was able to come up with a total traveling distance for the ten fixtures of 435 miles, a significant improvement on the 701 miles for the actual fixtures. The “average” away fan only had to travel 43.5 miles under my scheme, rather that the actual average away journey of 70 miles. However, I did end up with a number of derbies (e.g. Man United v Man City, Liverpool v Everton etc.) and it is possible that the schedulers wanted to save these key fixtures for another date.
And then I thought some more. What if I flipped my algorithm on its head and instead of considering the most remote team first (Swansea), I started by pairing the closest teams first. So this was my second algorithm:
- Find the closest pair of teams, write them down as a fixture and cross them out.
- Repeat step 1 until all teams are in a fixture.
And this yielded even better results: a total traveling distance of only 305 miles was needed for this set of fixtures (an average of 30.5 miles), although it was a little less egalitarian with a small number of teams having to travel longer distances. And this approach resulted in even more local derbies.
I’ve no idea if my latter method will always be the best, or my first gives the best balance of distance traveled and spread of distances, but I had a bit of fun figuring it all out and I’m sure I will continue to ponder the problem.
It also struck me that it would make quite a good investigation for the classroom – challenge the pupils to see who can come up with the fixtures that minimise the total traveling distances. You could leave it as open as that, requiring the students to find the distances between the various clubs and providing some good cross-curricula links with ICT and Geography, or you could provide the data yourself (when I get round to, I might put the data into a table for you). You could simplify the problem and reduce the number of teams (perhaps based on your own local area?) or an obvious extension question is: “Can you maximise the total traveling distances?”
If you do use the idea – either for your own enjoyment or in your classroom – do let me know. And if you do know of a “proper” algorithm for solving this problem I’d love to hear about it.
There’s a big block of fixtures on New Year’s Day – lets face it, who wants to go far on New Year’s Day? As you “recuperate” on your sofa on Thursday have a glance at the day’s football fixtures and see if you could have done a better job in arranging them.