“What’s the point?” the question we hear from students all too frequently. “When am I ever going to need this?” “Do I really need to know trigonometry?” Tricky questions, and I never feel satisfied with the answers I give my pupils.
Who knows when someone will use a trig ratio in later life, but that’s not really the point: learning maths is about training the mind to look at – and solve – problems in a methodical and logical way.
But its always good to find some “high school math” being used in real world solutions, and I stumbled across an example over the weekend.
A computer programmer needed to compare images and, in particular, see where the two images differed significantly, for example where a logo may have been superimposed upon an image.
Here’s the maths in a nutshell:
An image can be broken up into a load of pixels – essentially coloured points on an axis, and each point is identified by its (x,y) co-ordinates. All the points (pixels) when seen together make up the image.
It is the colour at each pixel that is important, and that colour is made up of red, green and blue – the amount of red, for example, is given by a value from 0 to 255, and the same fro green and blue. For example, the natty pink colour below is made up of 220 Red, 50 Green & 150 Blue:
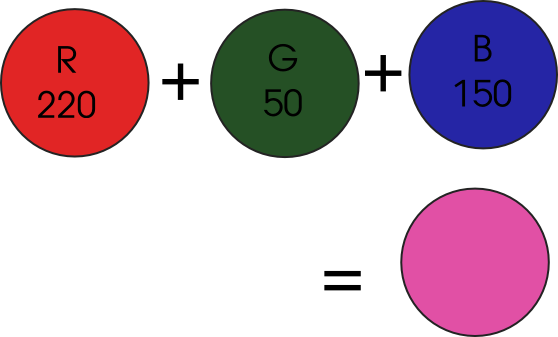So, to compare the two images, he took the equivalent pixels from each image and compared how close in colour each pixel was. And this is the really clever use of school boy maths. He used Pythagoras’ theorem, albeit in three dimensions, rather than two (you can use Pythagoras for as many different dimensions as he liked) to find the distance of the “colour” from the origin for each pixel. In our example the distance from the origin is the square root of
2202 + 502 + 1502 = 73400
√73400 = 270.9
He then compared the distances from the origin of the two pixels: if the distance was similar that part of the image was similar. He used a little bit of A Level Maths (Statistics) – Standard Deviation – to determine if the distances were “similar.”
Who would have though that Pythagoras’ Theorem could be use to see if two images are similar? The great Greek certainly wouldn’t have done, but the point is that the maths is fairly simple, its application brilliant. So when we teach trig or Pythagoras or algebra or geometry who knows how it will be applied next week, next month next millennia? And that’s the point – teaching maths equips the student with a tool-box, how they use that tool box in the future is up to them.
If you are interested in finding out more about the technique above, read the original article here – it’s quite techy and full of code (that I don’t profess to fully understand!) but you might find it useful.